Optimierung chemischer Prozesse


Dr. Patrick Bangert
algorithmica technologies GmbH
Die Effizienz und Wirtschaftlichkeit einer chemischen Werksanlage kann durch mathematische Modellierung optimiert werden. Die Optimierung erlaubt den Bediensteten der Anlage, solche Einstellungen (Soll-Werte) vorzunehmen, die eine maximale Wirtschaftlichkeit erreichen. Diese Methode erfordert keinerlei technische Modifikationen der Anlage. Wir werden zeigen, dass in einer Silan-produzierenden Chemieanlage eine Verbesserung der Wirtschaftlichkeit um ca. 6% möglich ist. Die Produktionsmenge konnte um 5,1% insgesamt und die des gewinnträchtigsten Endproduktes um 2,9% gesteigert werden.
Wie andere Branchen, ist auch die Chemie-Branche ständig darum bemüht, die Wirtschaftlichkeit ihrer Anlagen durch Mengensteigerungen zu verbessern. Solche Steigerungen können erzielt werden entweder durch technische Innovationen, die aber sehr kostenintensiv sind, oder durch Verhaltensänderungen im Betrieb. Diese Verhaltensänderungen können Menge und Gewinn steigern, ohne die Ausrüstung oder die Prozesse der Anlage zu verändern. Die Frage ist: Welche Änderungen sind nötig, um die Menge zu steigern? oder besser noch: um die Menge unter den gegebenen Umständen zu optimieren? Wir werden hier mit Hilfe von „maschinellem Lernen“ berechnen, welche Maßnahmen erforderlich sind, um die Menge unter den jeweiligen Gegebenheiten zu optimieren. Bei dieser Methode wird ein mathematisches Modell des Betriebsablaufes erstellt, das allein aufgrund vorhandener (historischer) Daten erstellt wird und deshalb schnell und wirtschaftlich eingesetzt werden kann.
Während manche kleinere Prozessabläufe dank verschiedener komplexer Technologien voll automatisiert sind, werden die allgemeinen Abläufe meistens vom Anlagenpersonal kontrolliert. Weil die Anlagenfahrer jedoch in Schichten arbeiten, kontrolliert kein einzelner von ihnen die Anlage über den gesamten Zeitraum, sondern kann dies jeweils nur für seine eigene Schicht tun. Es zeigt sich, dass die Effizienz der Anlage ungefähr von einer Acht-Stunden-Schicht zur nächsten schwankt, da von Menschen getroffene Entscheidungen einen erheblichen Einfluss auf die Effizienz der Anlage haben. Manche Fahrer sind besser als andere, und es ist auch nicht leicht, das Know-how und die Erfahrung der besten Fahrer auf andere zu übertragen, die weniger sachkundig und erfahren sind. Selbst wo Wissenstransfer-Systeme vorhanden sind, funktioniert dieser Wissenstransfer nur bis zu einem gewissen Grad, aber nicht immer optimal. Somit gibt es gute Anlagenfahrer und weniger gute.
Hinzu kommt, dass die Anlage gewöhnlich mehrere tausend Messwerte in häufigen Intervallen auswirft. Ein einzelner Anlagenfahrer kann unmöglich auch nur die wichtigsten dieser Messgrößen jederzeit im Auge behalten. Der Komplexitätsgrad ist für den menschlichen Geist meist zu groß, so dass auch von den besten Anlagenfahrern suboptimale Entscheidungen getroffen werden.
Die Herausforderung besteht somit darin, die Effizienz der Anlage durch eine Systematisierung der Arbeitsabläufe zu steigern, indem diese Abläufe weniger von der Intuition der Operateure abhängig bleiben als vielmehr von harten Fakten. Wie wird das gemacht?
Die Grundlage für das Optimierungs-Modell sind die historischen Daten des Archivsystems, das über die Zahlenwerte der verschiedenen Variablen Buch führt. Das Wissen und die Erfahrung der Anlagenfahrer schlagen sich deutlich in diesen Zahlen nieder. Ist die Historie dieser Daten lang und detailliert genug, kann dies als Hintergrundinformation völlig ausreichen. Wegen der überwältigen Datenmenge könnten diese Informationen für eine menschlichen Person keinen Lerneffekt bewirken. „Maschinelles Lernen“ ist hingegen geeignet, aus der Fülle der Daten ein diesem Zahlenmaterial zugrunde liegendes Muster zu erkennen und daraus eine einfache Gleichung zu erstellen, die uns als Entscheidungsgrundlage dienen kann.
Der Zweck der hier untersuchten chemischen Anlage ist es, ihr bestimmte chemische Stoffe (wie Silikon und diverse Wasserstoffverbindungen) zuzuführen, diese Stoffe dann einer Müller-Rochow-Synthese (siehe Schaubild 1) zu unterziehen, um daraus Di Methylchlorid Silane ((CH3)SiCl2) und Tri Methylchlorid Silane ((CH3)SiCl3) zu gewinnen. Nachfolgend sprechen wir von diesen beiden Produkten als Di und Tri.

Schaubild 1.: Aufriss einer Müller-Rochow-Synthese-Anlage: (A) Kompressor, (B) Zerstäuber, (C) Wirbelschichtreaktor, (D) Kühlmantel, (E) Zyklon, (F) Silikon/Kuper (Katalyst), (G) Methylchlorid, (H) Kondensator, (I) Roh-Silane, (J) zur Distillation, (K) Silikon/Kupfer-Asche, (L) Wärmetauscher, (M) Restbestand, und (N) Rückfluss Methylchlorid.
Ein Optimum an Wirtschaftlichkeit wird durch eine maximale Produktionsmenge aus einem Minimum an Rohstoffen erzielt. Die Selektivität bestimmter Endprodukte wird beeinflusst durch die Menge verschiedener hinzugefügter Katalysatoren und Promotorenstoffe sowie durch verschiedene Regelgrößen wie Temperatur und Druck. Das alles muss für die bestmöglichen Prozessabläufe austariert werden, wobei es auch auf eine Reihe von Merkmalen ankommt, die der Anlagenfahrer überhaupt nicht beeinflussen kann – wie die Außentemperatur oder die Qualität der Rohstoffe.
Zur Vereinfachung behandeln wir die ganze Anlage wie eine „Black Box“. Rohstoffe gehen in die Box hinein und Produktstoffe kommen aus der Box heraus. Die Box hat einige Messgeräte, mit deren Hilfe wir feststellen können, was sich innerhalb der Box abspielt, und es gibt auch einige Regler (Einstellvorrichtungen), mit denen wir beeinflussen können, was innerhalb der Box passiert. Aufgrund dieser Informationen wollen wir die Beziehung zwischen Input und Output bestimmen. Dabei berücksichtigen wir, dass wir die Messgeräte nur ablesen, aber nicht beeinflussen können, während wir die Regler beeinflussen können. Den Vorgang, mit dessen Hilfe wir die Beziehung zwischen Input und Output bestimmen können, nennen wir maschinelles Lernen, werden auf die Methode hier jedoch nicht näher eingehen. Wichtig zu wissen ist, dass dieses maschinelle Lernen automatisch erfolgt – ohne eine manuelle Beeinflussung durch menschliche Erfahrung. Maschinelles Lernen basiert ausschließlich auf den gesammelten (historischen) Daten der Anlage.
Das Ergebnis ist eine Reihe von Formeln, die beschreiben, was bei bestimmten Inputs, Regel-Vorgaben und Messwerten am Ende herauskommt. Diese Gleichungen können dann auch umgekehrt werden, so dass wir zu fragen in der Lage sind: Was sind die optimalen Regler-Einstellungen und optimalen Mengen der Input-Stoffe angesichts der derzeit vorhandenen Messwerte, die wir als gegeben annehmen müssen? Der Begriff optimal wird dabei definiert als die größte Wirtschaftlichkeit. Und die Antwort auf die obige Frage ist eine konkrete Handlungsanweisung, die vom Anlagenfahrer ausgeführt werden muss, um das Optimum zu erzielen.
Die Schlussfolgerungen der Optimierung ergaben sich nach einer experimentellen Phase, die drei Monate dauerte und drei Reaktoren umfasste. Während einer Evaluationsphase setzte der Anlagenfahrer nur solche vorgeschlagene Maßnahmen um, die er (oder sie) selbst für nützlich hielt. Während einer Anwendungsphase setzte er sämtliche Maßnahmen um, die das Computermodell berechnet hatte. Während einer Kontrollphase setzte er keinerlei Optimierungsmaßnahmen des Modells ein. Die Ergebnisse der drei Phasen befinden sich in Schaubild 2.
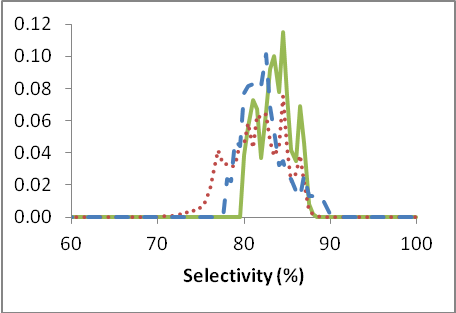
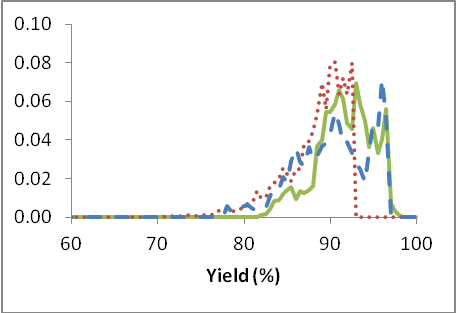
Figure 2.: Die Wahrscheinlichkeits-Verteilung für Selektivität und Menge für Di für die jeweiligen drei Phasen: Keine Optimierung (Kontrollphase: rot-gepunktete Linie), vom Fahrer als nützlich ausgewählte Optimierungsmaßnahmen (Evaluationsphase: blau-gestrichelte Linie) und Umsetzung aller vom Modell errechneten Maßnahmen (Anwendungsphase: grüne durchgezogene Linie).
Es zeigt sich, schon allein aufgrund dieser Darstellungen, dass wir Selektivität und Menge steigern können, wenn wir die Optimierung anwenden, und dass wir die Varianz (d.h. die Streuung der Ergebnisse) sowohl bei der Selektivität als auch beim Ertrag reduzieren können. Eine Reduzierung der Streuung ist deshalb wünschenswert, weil sich dadurch eine stabilere Reaktion über einen längeren Zeitraum ergibt und somit ein gleichförmiges Produkt generiert. In Zahlen ausgedrückt, werden die Ergebnisse in der Tabelle 1 unten aufgeführt.
Tabelle 1.: Für Selektivität und Ertrag haben wir die durchschnittliche Standardabweichung (+/-) für alle drei Phasen berechnet.
Die Ergebnisse zeigen, dass die Selektivität um ungefähr 2,9% gesteigert werden kann und der Ertrag um ca. 5,1% (jeweils absolut), wenn wir die Anwendungsphase mit der Kontrollphase vergleichen. Zusammengenommen, ergeben diese beiden Faktoren eine Steigerung der Wirtschaftlichkeit von ungefähr 6% für die Anlage.
Es muss betont werden, dass diese Steigerung der Wirtschaftlichkeit um 6% allein durch eine Verhaltensänderung der Anlagenfahrer ermöglicht wurde, die sich die berechnete Optimierung zunutze machten. Es war kein Investitionsaufwand nötig.
Die praktische Installation dieser Optimierung beanspruchte etwa zwei Tage der Arbeitszeit der Anlagenfahrer. Die Berechnungszeit, die der Computer benötigte, um die notwendigen Funktionen zu erstellen, belief sich auf etwa einen Monat. Die Computer-Schnittstellen, die erforderlich sind, um für Input und Output die nötigen Daten zu erheben, gehören in der Branche zur standardisierten Ausrüstung und können deshalb ohne Verzögerung zur Anwendung kommen.
Somit kann das Modell innerhalb eines Monats voll operationalisiert werden, ohne die Arbeitszeit der Anlagenführer über Gebühr zu strapazieren. Dieser Ansatz lässt sich also in einer realen Industrieanlage ohne Weiteres praktisch anwenden.